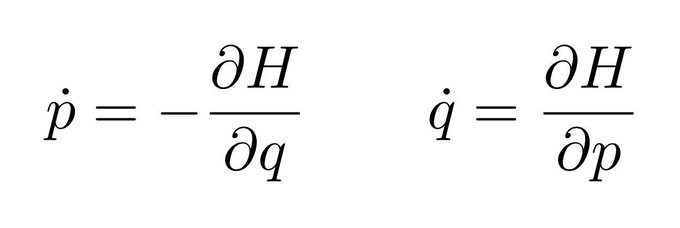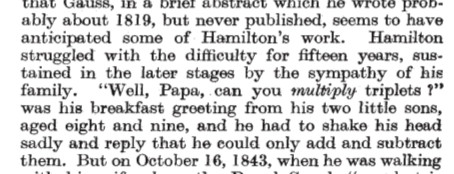I am so sorry.
Robert McNees
@mcnees.bsky.social
14597 Followers
684 Following
Professor and physicist. Black holes, quantum gravity, cosmology. Rocky Top. Tar Heel. Reposts are spooky action at a distance. These are my views, not my employer's. Just terrible at this.
Statistics
-
-
Anyway, I guess you could say that Hamilton was...
[puts on sunglasses]
...not throwing away his dot.
[steps on rake and hits self in face] (16/16)
-
Throughout his adult life, Hamilton reportedly struggled with alcohol. He abstained for two years after embarrassing himself at a meeting. But he took it up again after colleagues teased him for drinking water. Supposedly, excessive drinking brought on his fatal attack of gout. (15/n)
-
Hamilton was elected the first foreign member of the US National Academy of Sciences in 1864. He passed away the following year. (14/n)
-
For the longest time, he couldn't. Until one day he had a flash of insight while walking across a bridge with his wife:
i² = j² = k² = i j k = -1
He stopped and carved his formula for quaternions right there on the bridge. There's a plaque there now! (13/n)
Image: Wikipedia
-
Eventually he became fixated on the idea of endowing triplets of numbers with a similar structure to that of complex numbers. But he was stuck, and it was agony. Each morning, at breakfast, his children would ask "Well, Papa can you multiply triplets?" (12/n)
Ref: Piaggio, Nature 152, 1943
-
Around the same time, Hamilton read a paper that treated complex numbers as pairs of real numbers, or "algebraic couples."
He was intrigued, and for years considered ways of using and extending these quantities in his study of mechanics, optics, and other fields. (11/n)
-
There's a beautiful sort of geometry underlying all this that is known as symplectic structure. It's a rich field of mathematics. This formulation of classical mechanics was central to early formulations of quantum mechanics. (10/n)
-
Once you know the "Hamiltonian" H of the system –– in most of the examples we teach physics students it is essentially the total energy –– the q's (positions) and p's (momenta) evolve according to a simple pair of equation. (9/n)
-
Hamilton realized that this approach could be reframed in terms of positions and momenta, with the time evolution of the system given by pairs of first order differential equations. (8/n)